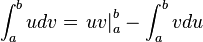resolved ésta integral por partes en vez de por cambio de variable y demostradle a mi profesor de matemáticas que yo estaba en lo cierto, puesto que al ser de la forma polinomio por ex lo primero que me vino a la mente fue el método por partes.
integral de x e-x2
os quiero.
no se puede, por partes: 
u= x
dv= e-x2
al intentar encontrar "vdu" te queda siempre el e-x2 por otra x lo que te impide integrar esa parte, tendrias que volverlo hacer por partes y asi infinitamente.
EDIT: ademas, no puedes hacer la integral de e-x2, asi que es imposible.
Tambien he visto esto :
It can't be integrated using integration by parts. If you choose u = x dv = ex2 dx then you can't find v since ex2 dx doesn't have an elementary integral; if you choose u = ex2 and dv = xdx than the new integral will be more complicated than the original one and you haven't gotten anywhere. But you can solve it fairly easy by substitution, say t = x2, that means that dt = 2xdx and xdx = dt/2, so you have ? 1/2 et dt = 1/2 et = 1/2ex2.
la funcion error no te la integrara realmente pero sirve para avanzar en el metodo por partes
junto a las series de taylor sirven para representar esa integral
es una puta integral inmmediata, repasad vuestros apuntes XDDDDDDDDDDDD
respuesta
edit: vale, me he leido #1 no, no puedes hacerla por partes.
si lo haces por aproximación de taylor si que se puede, pero no podras integrar esa funcion. lo que quiero decir esque no te quedara una funcion solamente con "x", podras obtener algo aproximado.
#10 evidentemente es eso, pero estamos discutiendo si se puede hacer por partes o no. yo digo que no.
wins the game.
Mira que sois....
Viendo #1.... creo que la pregunta es si aun existiendo una respuesta, se puede hacer por partes...
Es un tanto absurdo.... en el segundo término te quedaría la integral de la función error.... que sí, que la puedes calcular a malas numéricamente, pero es absurdo xDDD.
Despues del primer paso te queda:
= Constantes * x * errf(x) - Constantes*Int (errf(x) dx)
....
Menudo avance xD.
EDIT:
fail mio, int (erfc(x)) esta definida:
xerrfc(x) - Constantes(e-(X2))
Asi que sería:
INT = Axerfc(x)-Bxerfc(x)+Cexp(-xx)
A, B y C te las calculas tú.
EDIT2:
Más fail mio,
A y B son iguales y C = -1/2, osea, que por partes, como debe ocurrir, sale exactamente #10.
Concluyendo, sí, se puede hacer por partes, y te da #10 XD Pero #10 es inmediata.
Bien, resumiendo el cálculo más absurdo de mi existencia...
Usando la definición de erf(x) y la de integral de erf(x) se puede recuperar #10 "por partes".... es absurdo, pero oye, si #1 es feliz:
#1= x* 1/2sqrt(pi)erf(x)-1/2sqrt(pi)int[erf(x)*dx]------ despues de integrar por partes
Usando que int[erf(x)dx] = xerf(x)+exp(-x*x)/sqrt(pi) te queda
#1 = x1/2sqrt(pi)erf(x)-x1/2sqrt(pi)erf(x)-1/2sqrt(pi)/sqrt(pi)exp(-x*x) = #10
